Fiber Bragg grating

A fiber Bragg grating (FBG) is a type of distributed Bragg reflector constructed in a short segment of optical fiber that reflects particular wavelengths of light and transmits all others. This is achieved by creating a periodic variation in the refractive index of the fiber core, which generates a wavelength specific dielectric mirror. A fiber Bragg grating can therefore be used as an inline optical filter to block certain wavelengths, or as a wavelength-specific reflector.

History

The first in-fiber Bragg grating was demonstrated by Ken Hill in 1978.^[1] Initially, the gratings were fabricated using a visible laser propagating along the fiber core. In 1989, Gerald Meltz and colleagues demonstrated the much more flexible transverse holographic inscription technique where the laser illumination came from the side of the fiber. This technique uses the interference pattern of ultraviolet laser light^[2] to create the periodic structure of the fiber Bragg grating.

Manufacture

Fiber Bragg gratings are created by "inscribing" or "writing" systematic (periodic or aperiodic) variation of refractive index into the core of a special type of optical fiber using an intense ultraviolet (UV) source such as a UV laser. Two main processes are used: interference and masking. The method that is preferable depends on the type of grating to be manufactured. Normally a germanium-doped silica fiber is used in the manufacture of fiber Bragg gratings. The germanium-doped fiber is photosensitive, which means that the refractive index of the core changes with exposure to UV light. The amount of the change depends on the intensity and duration of the exposure as well as the photosensitivity of the fibre. To write a high reflectivity fiber Bragg grating directly in the fiber the level of doping with germanium needs to be high. However, standard fibers can be used if the photosensitivity is enhanced by pre-soaking the fiber in hydrogen. More recently, fiber Bragg gratings have also been written in polymer fibers, this is described in the PHOSFOS entry ^[3].

Interference

The was the first method used widely for the fabrication of fiber Bragg gratings and uses two-beam interference. Here the UV laser is split into two beams which interfere with each other creating a periodic intensity distribution along the interference pattern. The refractive index of the photosensitive fiber changes according to the intensity of light that it is exposed to. This method allows for quick and easy changes to the Bragg wavelength, which is directly related to the interference period and a function of the incident angle of the laser light.

Photomask

A photomask having the intended grating features may also be used in the manufacture of fiber Bragg gratings. The photomask is placed between the UV light source and the photosensitive fiber. The shadow of the photomask then determines the grating structure based on the transmitted intensity of light striking the fiber. Photomasks are specifically used in the manufacture of chirped Fiber Bragg gratings, which cannot be manufactured using an interference pattern.

Point-by-point

A single UV laser beam may also be used to 'write' the grating into the fiber point-by-point. Here, the laser has a narrow beam that is equal to the grating period. This method is specifically applicable to the fabrication of long period fiber gratings. Point-by-point is also used in the fabrication of tilted gratings.

Production

Originally, the manufacture of the photosensitive optical fiber and the 'writing' of the fiber Bragg grating were done separately. Today, production lines typically draw the fiber from the preform and 'write' the grating, all in a single stage. As well as reducing associated costs and time, this also enables the mass production of fiber Bragg gratings. Mass production is in particular facilitating applications in smart structures utilizing large numbers (3000) of embedded fiber Bragg gratings along a single length of fiber.

Theory

The fundamental principle behind the operation of a FBG, is Fresnel reflection. Where light traveling between media of different refractive indices may both reflect and refract at the interface.

The grating will typically have a sinusoidal refractive index variation over a defined length. The reflected wavelength (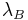 $\lambda_B$ ), called the Bragg wavelength, is defined by the relationship,

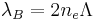$\lambda_B= 2 n_e \Lambda\,$ ,

where 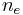$n_e$ is the effective refractive index of the grating in the fiber core and 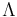$\Lambda$ is the grating period. The effective refractive index quantifies the velocity of propagating light as compared to its velocity in vacuum. 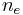$n_e$ depends not only on the wavelength but also (for multimode waveguides) on the mode in which the light propagates. For this reason, it is also called modal index.

The wavelength spacing between the first minima (nulls, see Fig. 2), or the bandwidth (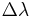 $\Delta\lambda$ ), is (in the strong grating limit) given by,

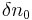$\Delta \lambda=\left[\frac{2 \delta n_0 \eta}{\pi}\right]\lambda_B$ ,

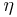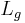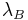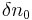where $\delta n_0$ is the variation in the refractive index ( $n_3-n_2$ ), and $\eta$ is the fraction of power in the core. Note that this approximation does not apply to weak gratings where the grating length, $L_g$ , is not large compared to $\lambda_B$ \ $\delta n_0$ .

The peak reflection (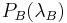 $P_B(\lambda_B)$ ) is approximately given by,

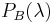$P_B(\lambda_B) \approx \tanh^2 \left[\frac{N \eta (V) \delta n_0}{n}\right]$ ,

where $N$ is the number of periodic variations. The full equation for the reflected power ( $P_B(\lambda)$ ), is given by,

$P_B(\lambda) = \frac{\sinh^2\left[ \eta (V) \delta n_0 \sqrt{1-\Gamma^2} N \Lambda / \lambda\right]}{\cosh^2\left[\eta (V) \delta n_0 \sqrt{1-\Gamma^2} N \Lambda / \lambda\right]-\Gamma^2}$ ,

where,

$\Gamma (\lambda)=\frac{1}{\eta (V) \delta n_0}\left[\frac{\lambda}{\lambda_B}-1\right]$ .

Types of gratings

The term “type” in this context refers to the underlying photosensitivity mechanism by which grating fringes are produced in the fiber. The different methods of creating these fringes have a significant effect on physical attributes of the produced grating, particularly the temperature response and ability to withstand elevated temperatures. Thus far, five (or six) types of FBG have been reported with different underlying photosensitivity mechanisms.^[4] These are summarized below:

Standard gratings or Type I gratings

Written in both hydrogenated and non-hydrogenated fiber of all types Type I gratings are usually known as standard gratings and are manufactured in fibers of all types under all hydrogenation conditions. Typically, the reflection spectra of a type I grating is equal to 1-T where T is the transmission spectra. This means that the reflection and transmission spectra are complementary and there is negligible loss of light by reflection into the cladding or by absorption. Type I gratings are the most commonly used of all grating types, and the only types of grating available off-the-shelf at the time of writing.

Type IA gratings

Regenerated grating written after erasure of a type I grating in hydrogenated germanosilicate fiber of all types

Type IA gratings were first published in 2001^[5] during experiments designed to determine the effects of hydrogen loading on the formation of IIA gratings in germanosilicate fiber. In contrast to the anticipated blue shift of the peak Bragg wavelength, a large positive wavelength shift was measured. This type IA grating appeared once the conventional type I FBG had reached saturation followed by subsequent complete or partial erasure, and was therefore labeled as regenerated. It was also noted that the temperature coefficient of the regenerated grating was lower than a standard grating written under similar conditions.

There is a clear relationship between type IA and IIA gratings insomuch as their fabrication conditions are identical in all but one aspect: they both form in B/Ge co-doped fiber but IAs form only in hydrogenated fibers and IIAs form only in non-hydrogenated fibers.^[5]^[6]^[7]

Type IIA (Also known as Type In gratings)

These are gratings that form as the negative part of the induced index change overtakes the positive part. It is usually associated with gradual relaxation of induced stress along the axis and/or at the interface. It has been proposed that these gratings could be relabeled Type In (for Type 1 gratings with a negative index change; Type II label could be reserved for those that are distinctly made above the damage threshold of the glass).^[8]

Later research by Xie et al. showed the existence of another type of grating with similar thermal stability properties to the type II grating. This grating exhibited a negative change in the mean index of the fiber and was termed type IIA. The gratings were formed in germanosilicate fibers with pulses from a frequency doubled XeCl pumped dye laser. It was shown that initial exposure formed a standard (type I) grating within the fiber which underwent a small red shift before being erased. Further exposure showed that a grating reformed which underwent a steady blue shift whilst growing in strength.^[9]^[10]

Regenerated gratings

These are gratings that are reborn at higher temperatures after erasure of gratings, usually Type I gratings and usually, though not always, in the presence of hydrogen. They have been interpreted in different ways including dopant diffusion (oxygen being the most popular current interpretation) and glass structural change. Recent work has shown that there exists a regeneration regime beyond diffusion where gratings can be made to operate at temperatures in excess of 1295C, outperforming even Type II femtosecond gratings.^[11] These are extremely attractive for ultra high temperature applications.

Type II gratings

Damage written gratings inscribed by multiphoton excitation with higher intensity lasers that exceed the damage threshold of the glass. Lasers employed are usually pulsed in order to reach these intensities. They include recent developments in multiphoton excitation using femtosecond pulses where the short timescales (commensurate on a timescale similar to local relaxation times) offer unprecedented spatial localization of the induced change. The amorphous network of the glass is usually transformed via a different ionization and melting pathway to give either higher index changes or create, through micro-explosions, voids surrounded by more dense glass.

Archambault et al. showed that it was possible to inscribe gratings of ~100% (>99.8%) reflectance with a single UV pulse in fibers on the draw tower. The resulting gratings were shown to be stable at temperatures as high as 800˚C (up to 1000C in some cases, and higher with femtosecond laser inscription). The gratings were inscribed using a single 40mJ pulse from an excimer laser at 248 nm. It was further shown that a sharp threshold was evident at ~30mJ; above this level the index modulation increased by more than two orders of magnitude, whereas below 30mJ the index modulation grew linearly with pulse energy. For ease of identification, and in recognition of the distinct differences in thermal stability, they labeled gratings fabricated below the threshold as type I gratings and above the threshold as type II gratings. Microscopic examination of these gratings showed a periodic damage track at the grating’s site within the fiber [10]; hence type II gratings are also known as damage gratings. However, these cracks can be very localized so as to not play a major role in scattering loss if properly prepared ^[12]^[13]

Grating structure

The structure of the FBG can vary via the refractive index, or the grating period. The grating period can be uniform or graded, and either localised or distributed in a superstructure. The refractive index has two primary characteristics, the refractive index profile, and the offset. Typically, the refractive index profile can be uniform or apodized, and the refractive index offset is positive or zero.

There are six common structures for FBGs;^[14]

uniform positive-only index change,
Gaussian apodized,
raised-cosine apodized,
chirped,
discrete phase shift, and
superstructure.

The first complex grating was made by J. Canning in 1994.^[15] This supported the development of the first distributed feedback (DFB) fiber lasers, and also laid the groundwork for most complex gratings that followed, including the sampled gratings first made by Peter Hill and colleagues in Australia.

Apodized gratings

There are basically two quantities that control the properties of the FBG. These are the grating length, 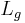$L_g$ , given as

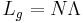$L_g=N\Lambda\,$ ,

and the grating strength, 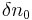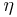$\delta n_0$ $\eta$ . There are, however, three properties that need to be controlled in a FBG. These are the reflectivity, the bandwidth, and the side-lobe strength. As shown above, in the strong grating limit (i.e. for large 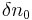$\delta n_0$ ) the bandwidth depends on the grating strength, and not the grating length. This means the grating strength can be used to set the bandwidth. The grating length, effectively $N$ , can then be used to set the peak reflectivity, which depends on both the grating strength and the grating length. The result of this is that the side-lobe strength cannot be controlled, and this simple optimisation results in significant side-lobes. A third quantity can be varied to help with side-lobe suppression. This is apodization of the refractive index change. The term apodization refers to the grading of the refractive index to approach zero at the end of the grating. Apodized gratings offer significant improvement in side-lobe suppression while maintaining reflectivity and a narrow bandwidth. The two functions typically used to apodize a FBG are Gaussian and raised-cosine.

Chirped fiber Bragg gratings

The refractive index profile of the grating may be modified to add other features, such as a linear variation in the grating period, called a chirp. The reflected wavelength changes with the grating period, broadening the reflected spectrum. A grating possessing a chirp has the property of adding dispersion—namely, different wavelengths reflected from the grating will be subject to different delays. This property has been used in the development of phased-array antenna systems and polarization mode dispersion compensation, as well.

Tilted fiber Bragg gratings

In standard FBGs, the grading or variation of the refractive index is along the length of the fiber (the optical axis), and is typically uniform across the width of the fiber. In a tilted FBG (TFBG), the variation of the refractive index is at an angle to the optical axis. The angle of tilt in a TFBG has an effect on the reflected wavelength, and bandwidth.

Long-period gratings

Typically the grating period is the same size as the Bragg wavelength, as shown above. For a grating that reflects at 1500 nm, the grating period is 500 nm, using a refractive index of 1.5. Longer periods can be used to achieve much broader responses than are possible with a standard FBG. These gratings are called long-period fiber grating. They typically have grating periods on the order of 100 micrometers, to a millimeter, and are therefore much easier to manufacture.

Applications

Communications

The primary application of fiber Bragg gratings is in optical communications systems. They are specifically used as notch filters. They are also used in optical multiplexers and demultiplexers with an optical circulator, or Optical Add-Drop Multiplexer (OADM). Figure 5 shows 4 channels, depicted as 4 colours, impinging onto a FBG via an optical circulator. The FBG is set to reflect one of the channels, here channel 4. The signal is reflected back to the circulator where it is directed down and dropped out of the system. Since the channel has been dropped, another signal on that channel can be added at the same point in the network.

A demultiplexer can be achieved by cascading multiple drop sections of the OADM, where each drop element uses a FBG set to the wavelength to be demultiplexed. Conversely, a multiplexer can be achieved by cascading multiple add sections of the OADM. FBG demultiplexers and OADMs can also be tunable. In a tunable demultiplexer or OADM, the Bragg wavelength of the FBG can be tuned by strain applied by a piezoelectric transducer. The sensitivity of a FBG to strain is discussed below in fiber Bragg grating sensors.

Fiber Bragg grating sensors

As well as being sensitive to strain, the Bragg wavelength is also sensitive to temperature. This means that fiber Bragg gratings can be used as sensing elements in optical fiber sensors. In a FBG sensor, the measurand causes a shift in the Bragg wavelength, 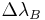$\Delta \lambda_B$ . 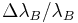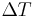The relative shift in the Bragg wavelength, $\Delta \lambda_B/\lambda_B$ , due to an applied strain ( $\epsilon$ ) and a change in temperature ( $\Delta T$ ) is approximately given by,

$\left[\frac{\Delta \lambda_B}{\lambda_B}\right]= C_S\epsilon %2B C_T\Delta T$ ,

or,

$\left[\frac{\Delta \lambda_B}{\lambda_B}\right]= (1-p_e)\epsilon %2B (\alpha_\Lambda %2B \alpha_n)\Delta T$ .

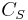Here, $C_S$ is the coefficient of strain, which is related to the strain optic coefficient 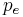$p_e$ . Also, 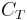$C_T$ is the coefficient of temperature, which is made up of the thermal expansion coefficient of the optical fiber, 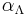$\alpha_\Lambda$ , and the thermo-optic coefficient, 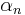$\alpha_n$ .^[16]

Fiber Bragg gratings can then be used as direct sensing elements for strain and temperature. They can also be used as transduction elements, converting the output of another sensor, which generates a strain or temperature change from the measurand, for example fiber Bragg grating gas sensors use an absorbent coating, which in the presence of a gas expands generating a strain, which is measurable by the grating. Technically, the absorbent material is the sensing element, converting the amount of gas to a strain. The Bragg grating then transduces the strain to the change in wavelength.

Specifically, fiber Bragg gratings are finding uses in instrumentation applications such as seismology,^[17] pressure sensors for extremely harsh environments, and as downhole sensors in oil and gas wells for measurement of the effects of external pressure, temperature, seismic vibrations and inline flow measurement. As such they offer a significant advantage over traditional electronic gauges used for these applications in that they are less sensitive to vibration or heat and consequently are far more reliable. In the 1990s, investigations were conducted for measuring strain and temperature in composite materials for aircraft and helicopter structures.^[18]^[19]

References

^ Hill, K.O.; Fujii, Y.; Johnson, D. C.; Kawasaki, B. S. (1978). "Photosensitivity in optical fiber waveguides: application to reflection fiber fabrication". Appl. Phys. Lett. 32 (10): 647. Bibcode 1978ApPhL..32..647H. doi:10.1063/1.89881.
^ Meltz, G.; et al. (1989). "Formation of Bragg gratings in optical fibers by a transverse holographic method". Opt. Lett. 14 (15): 823. Bibcode 1989OptL...14..823M. doi:10.1364/OL.14.000823. PMID 19752980.
^ http://www.phosfos.eu/eng/Phosfos/Journals/Bragg-grating-in-polymer-optical-fibre-for-strain-bend-and-temperature-sensing
^ J. Canning, Fiber Gratings and Devices for Sensors and Lasers, Lasers and Photonics Reviews, 2 (4), 275-289, Wiley, USA (2008)
^ ^a ^b Liu, Y. (2001). Advanced fiber gratings and their application. Ph.D. Thesis, Aston University.
^ Simpson, A. G. (2005). Optical Fibre Sensors and Their Interrogationdv. Ph.D. Thesis, Aston University.
^ Simpson, A. G.; Kalli, K.; Zhou, K.; Zhang, L.; Bennion, I. (2003). "A method for the fabrication of temperature compensating IA-I strain sensors". OFS16. Nara, Japan. pp. postdeadline paper PD4.
^ For a contemporary review, see J. Canning, Fiber Gratings and Devices for Sensors and Lasers, Lasers and Photonics Reviews, 2 (4), 275-289, Wiley, USA (2008)
^ Xie, W. X.; Niay, P.; Bernage, P.; Douay, M.; Bayon, J. F.; Georges, T.; Monerie, M.; Poumellec, B. (1993). "Experimental-Evidence of 2 Types of Photorefractive Effects Occurring During Photo inscriptions of Bragg Gratings Within Germanosilicate Fibres". Optics Communications 104 (1-3): 185–195. Bibcode 1993OptCo.104..185X. doi:10.1016/0030-4018(93)90127-Q.
^ Niay, P.; Bernage, P.; Legoubin, S.; Douay, M.; Xie, W. X.; Bayon, J. F.; Georges, T.; Monerie, M.; Poumellec, B. (1994). "Behaviour of Spectral Transmissions of Bragg Gratings Written in Germania-Doped Fibres - Writing and Erasing Experiments Using Pulsed or CW UV Exposure". Optics Communications 113 (1-3): 176–192. Bibcode 1994OptCo.113..176N. doi:10.1016/0030-4018(94)90606-8.
^ J. Canning, M. Stevenson, S. Bandyopadhyay, K. Cook, “Extreme silica optical fibre gratings”, Sensors, 8, pp.1-5, (2008)
^ Dong, L.; Archambault, J. L.; Reekie, L.; Russell, P. S. J.; Payne, D. N. (1993). "Single-Pulse Bragg Gratings Written During Fibre Drawing". Electronics Letters 29 (17): 1577–1578. doi:10.1049/el:19931051.
^ Archambault, J. L.; Reekie, L.; Russell, P. S. J. (1993). "100-Percent Reflectivity Bragg Reflectors Produced in Optical Fibres By Single Excimer-Laser Pulses". Electronics Letters 29 (5): 453–455. doi:10.1049/el:19930303.
^ Erdogan, Turan (August 1997). "Fiber Grating Spectra". Journal of Lightwave Technology 15 (8): 1277–1294. Bibcode 1997JLwT...15.1277E. doi:10.1109/50.618322. http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?tp=&arnumber=618322&isnumber=13456.
^ J. Canning, M. G. Sceats, "p-phase-shifted periodic distributed structures in germanosilicate fibre by UV post-processing", Electron. Lett., 30, (16), 1344-1345, (1994)
^ Othonos, Andreas; Kalli, Kyriacos (1999). Fiber Bragg Gratings: Fundamentals and Applications in Telecommunications and Sensing. Artech House. ISBN 0890063443.
^ P. Ferraro; G. De Natale (2002). "On the possible use of optical fiber Bragg gratings as strain sensors for geodynamical monitoring". Optics and Lasers in Engineering 37 (2-3): 115–130. Bibcode 2002OptLE..37..115F. doi:10.1016/S0143-8166(01)00141-5.
^ US patent 5493390, "Integrated optical instrumentation for the diagnostics of parts by embedded or surface attached optical sensors", issued Feb. 20, 1996
^ US patent 5399854, J.R. Dunphy & et al., "Embedded optical sensor capable of strain and temperature measurement using a single diffraction grating", issued March 21, 1995

External links

International Optical Sensor Societies

FOSNE - Fibre Optic Sensing Network Europe

Development Platforms

TFT - Technobis Fibre Technologies

Other

Bragg grating as hydrogen detector
http://www.patentgenius.com/patent/7133582.html - Fiber - Optic filter with tunable grating